Linear Block codes | Information Theory and Coding

(n, k) Block codes

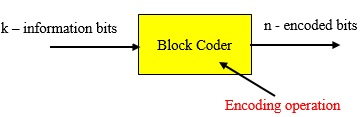
n-digit codeword made up of k-information digits and (n-k) redundant parity check digits. The rate or efficiency for this code is k/n.

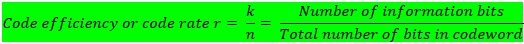
Note: unlike source coding, in which data is compressed, here redundancy is deliberately added, to achieve error detection.

SYSTEMATIC BLOCK CODES

A systematic block code consists of vectors whose 1^st k elements (or last k-elements) are identical to the message bits, the remaining (n-k) elements being check bits. A code vector then takes the form:

X = (m₀, m₁, m₂,……m_k-1, c₀, c₁, c₂,…..c_n-k)

Or

X = (c₀, c₁, c₂,…..c_n-k, m₀, m₁, m₂,……m_k-1)

Systematic code: information digits are explicitly transmitted together with the parity check bits. For the code to be systematic, the k-information bits must be transmitted contiguously as a block, with the parity check bits making up the code word as another contiguous block.

Systematic codewords are sometimes written so that the message bits occupy the left-hand portion of the codeword and the parity bits occupy the right-hand portion.

Parity check matrix (H)

Will enable us to decode the received vectors. For each (kxn) generator matrix G, there exists an (n-k)xn matrix H, such that rows of G are orthogonal  to rows of H i.e., GH^T = 0, where H^T is the transpose of H. to fulfil the orthogonal requirements for a systematic code, the components of H matrix are written as: H = [I_n-k | P^T]

In a systematic code, the 1^st k-digits of a code word are the data message bits and last (n-k) digits are the parity check bits, formed by linear combinations of message bits m₀, m₁, m₂,…….m_k-1

It can be shown that performance of systematic block codes is identical to that of non-systematic block codes.

A codeword (X) consists of n digits x₀, x₁, x₂, ……x_n-1 and a data word (message word) consists of k digits m₀, m₁, m₂,……m_k-1

For the general case of linear block codes, all the n digits of X are formed by linear combinations (modulo-2 additions) of k message bits. A special case, where x₀ = m₀, x₁ = m₁, x₂ = m₂….x_k-1 = mk-1 and the remaining digits from x_k+1 to x_n are linear combinations of m₀, m₁, m₂, ….. m_k-1 is known as a systematic code.

The codes described in this chapter are binary codes, for which the alphabet consists of symbols 0 and 1 only. The encoding and decoding functions involve the binary arithmetic operations of modulo-2 addition and multiplication.

Matrix representation of Block codes

• An (n, k) block code consists of n-bit vectors
• Each vector corresponding to a unique block of k-message bits
• There are 2^k different k-bit message blocks & 2ⁿ possible n-bit vectors
• The fundamental strategy of block coding is to choose the 2^k code vectors such that the minimum distance is as large as possible. In error correction, distance of two words (of same length) plays a fundamental role.

Block codes in which the message bits are transmitted in unaltered form are called systematic code.