Random Variable | Probability Theory

Variable

Variable is a symbol that can take on any number of specified set of values. Use capital letter to represent a RV and lowercase letter to represent one of its values.

Random variable

A random variable is a set of possible values from a random experiment. A random variable can assume several set of possible values. These possible values are numerical outcomes of a random experiment. Note that random variable is a quantity, whose value is subject to change. Note that the outcome of a random experiment cannot be predicted with certainty, before the experiment is run.

Let X = random variable

x = value of random variable

P(X) = Probability of random variable X

P(X=1) = Probability of RV, whose value is 1

P(X=5) = Probability of RV, whose value is 5

Random Variable: usually written as X, whose possible values are numerical outcomes of a random experiment

RV is also known as STOCHASTIC variable. A random variable is generally denoted by a capital letter X, Y, Z etc. A random variable takes on numerical values as the result of an experiment.

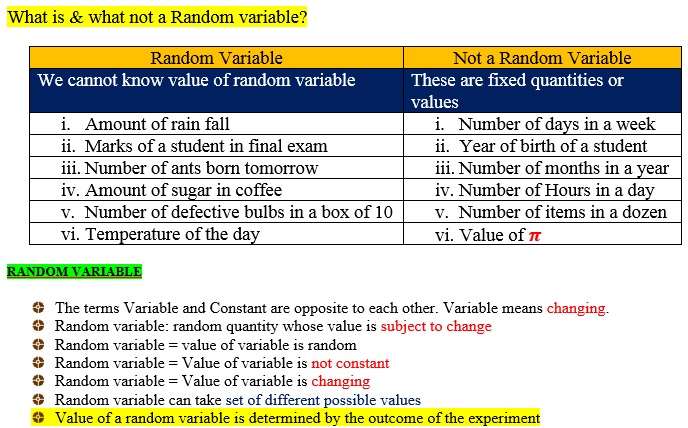
The word random means unpredictable, uncertain, in-deterministic. We call random because it can take several different possible values. Note that process of observation is referred to as an experiment. An experiment is called random experiment if its outcome can’t be predicted. Result of an experiment is known as outcome of experiment.

Other random variables that can be defined on this Sample Space (SS) are:

• The square of number of heads
• The number of heads minus number of tails etc.

Example: Coin toss 3 times.

Let X represents a random variable. Each random variable has some definition. Here X = ‘number of heads in the random variable’. So, possible values of X are: 0,1,2,3.

Example: Two dice are tossed

Let X = ‘sum of squares on the dice’. So, possible values of X are: X = {2,3,4,5,6,7,8,9,10,11,12}