Solved problems | Probability Theory

HOMEWORK PROBLEMS

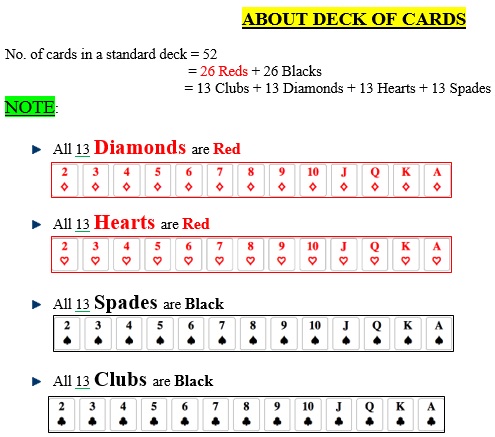
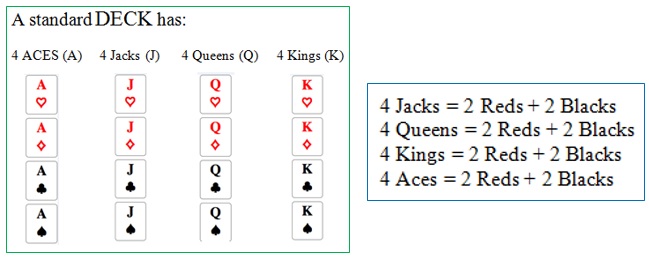
1. Determine probability P for each of the following events:  (a) A King, Ace, Jack or Queen of diamonds appears in drawing a single card from a well-shuffled ordinary deck of cards. (b). The sum 8 appears in a single toss of a pair of fair dice. (c). At least 1 head appears in 3 tosses of a fair coin.
2. Find the probability of drawing 3 aces at random from a deck of 52 ordinary cards if the cards are:
   1. Replaced
   2. Not replaced
3. A sample space consists of 3 sample points with associated probabilities given by 2p, p², and 4(p-1). Find the value of p.
4. Find the probability of a 4 turning up at least once in two tosses of a fair die.
5. A marble is drawn at random from a box containing 10 red, 30 white, 20 blue and 15 orange marbles. Find the probability that it is:
   1. Orange or red
   2. Not red or blue
   3. Not blue
   4. White
   5. Red, white or blue
6. A box contains 2 red and 3 blue marbles. Find the probability that if two marbles are drawn at random (without replacement),
   1. Both are blue
   2. Both are red
   3. One is red and one is blue
7. The number of different arrangements, or permutations, consisting of 3 letters each that can be formed from the 7 letters A, B, C, D, E, F, G is?
8. A machine produces a total of 12,000 bulbs a day, which are on an average3% defective. Find the probability that out of 600 bulbs chosen at random, 12 will be defective.
9. An urn contains 6 red and 8 blue marbles. Five marbles are drawn at random from it without replacement. Find the probability that 3 are red and 2 are blue.
10. An urn contains 4 white balls and six red ones. What is the probability that one ball drawn at random will be white?
11. Distinguish between the terms ‘mutually exclusive’ and ‘statistically independent events’
12. Write down Baye’s theorem and explain meaning of each term in the relation.